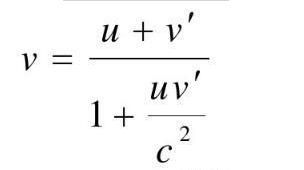关于量子纠缠,很多人都用一双手套来理解,那么本文也就用手套这个例子来给大家简单科普一下,为什么量子纠缠这么神奇。
想象一下,在不做观测的前提下,把一双手套分别装进两个盒子里,然后将这两个盒子分别送到很遥远的地方,比如说一个在地球上的某处,另一个被送到月球。这时你在地球上把这个盒子打开,如果你发现盒子里的手套是左手,那么你马上就会知道月球上的盒子是右手,反之亦然。
这好像就解释了量子纠缠的本质,但事实却不是这样。因为在量子纠缠的定义中,这两只手套是属于“既是左手、又是右手”的量子叠加态,你在观测地球上的这只手套的时候,这只手套的左或者右就被确定下来,而另一只手套就会根据你的观测结果确定自己的状态。
但是这似乎还是说不通,因为在这一双手套装进盒子之前,它们的左右就已经确定了,只是观测者自己不知道而已,哪来的“既是左手、又是右手”这种说法呢?
按照常识来讲,确实应该是这样的,爱因斯坦也是这么想的,他认为“上帝不会掷骰子”,宇宙是确定的,而所谓的量子纠缠现象,很可能是因为有某种我们暂时未知的“隐变量”。比如说一双正常的手套本来就是一只是左手,一只是右手,我们就可以将其简单地理解为,这就是手套的“隐变量”。
当年以爱因斯坦和玻尔为代表的两大阵营为此展开了激烈的争辩,谁也说不服谁。但在后来的日子里,量子力学渐渐占了上风,这时爱因斯坦的忠实粉丝-约翰.斯图尔特.贝尔(JohnStewartBell)坐不住了,他于1964年提出了大名鼎鼎的“贝尔不等式”,希望用实验来证明爱因斯坦是正确的。
这个“贝尔不等式”到底讲的是什么?为了帮助大家了解,这里还是用手套来举例说明。假设一个屋子里有一大堆的手套,它们分别有三种属性,即红或者蓝、左或者右、有花纹或者没有花纹(只能二取一),但是我们没有去观测它们。
按照爱因斯坦的想法,这些手套的三种属性都是事先就确定好了,那么当我们观测这些手套的时候,就可以得出一个结论:即红色的右手套加上有花纹的左手套的数量,总是大于或者等于红色的、有花纹的手套的数量。
大家不妨仔细思考一下,正常情况下,这个不等式是绝对成立的,只有当这些手套处于“叠加态”,同时又处于“纠缠态”的情况下,“贝尔不等式”才会不成立。
在实验中,这三种属性分别用光子的下、下自旋以及光的偏振性来代替,实验过程是将大量的处于纠缠态的光子发送到不同的地方,然而对它们进行分别观测,并统计观测数据,以此来验证“贝尔不等式”。
由于实验要求的条件非常高,这样的实验直到上世纪70年代才开始进行,随着实验精度的不断提高,越来越多的实验结果,都证实了量子力学所预测的结果是正确的,例如有名的“阿斯派克特实验”、“因斯布鲁克实验”等等。
事实证明,在量子纠缠的领域,爱因斯坦错了,世界上真的存在着“幽灵般的超距作用”,两个处于纠缠状态的量子,其中的一个如果被确定了,那么不管相距多远,另一个马上就会做出相对应的改变!